問題 2
ライフプランニングにおける各種係数を用いた必要額の算出に関する次の記述の空欄(ア)、(イ)にあてはまる語句の組み合わせとして、最も適切なものはどれか。なお、算出に当たっては下記<資料>の係数を乗算で使用し、手数料や税金等については考慮しないものとする。
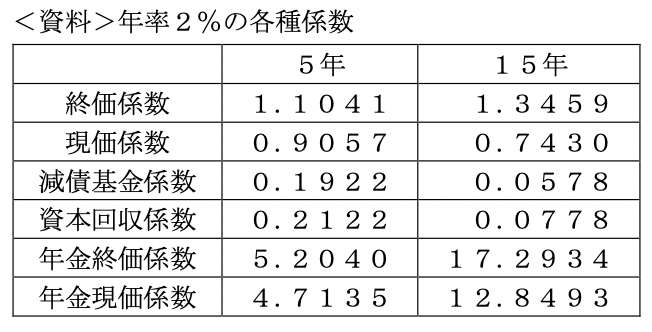
・ Aさんが60歳から65歳になるまでの5年間、年率2%で複利運用しながら、毎年200万
円を受け取る場合、60歳時点の元金として( ア )が必要となる。
・ Bさんが45歳から毎年一定額を積み立てながら年率2%で複利運用し、15年後の60歳時
に1,000万円を準備する場合、毎年の積立金額は( イ )となる。
1.(ア)9,057,000円 (イ)578,000円
2.(ア)9,057,000円 (イ)778,000円
3.(ア)9,427,000円 (イ)578,000円
4.(ア)9,427,000円 (イ)778,000円
解答
正解は3です。
解説
本問題は各種係数に関する問題です。
年利2%で複利運用しながら、5年間毎年200万円を取り崩すために、今いくら必要か?ということですから、これを計算式に表すと、
毎年受け取る年金額(取り崩す額)×年金現価係数=元金となります。
※ちなみに年金現価係数は、元本を一定利率で複利運用しながら毎年一定額を取り崩す場合、現在の元本がいくら必要かを計算するときに使います。
よって、200万円×4.7135=942.7万円
次に、15年間年利2%で複利運用しながら、目標額1,000万円を積み立てる場合に、必要な毎年の積立額はいくらか?ということですから、これを計算式に表すと、
目標額×減債基金係数=毎年の積立額
※減債基金係数は、一定期間一定利率で複利運用しながら目標額を積み立てる場合、毎年いくら積み立てるかを計算するときに使います。
よって、1,000万円×0.0578=57.8万円
よって正解は、3となります。

