次の文のア 及び イ に入る数値の組合せとして最も適当なものはどれか。次の中から選べ。
なお、関数の値が必要な場合は、巻末の関数表を使用すること。
三角形ABCで∠ABCの角度を同じ条件で5回測定し、表3の結果を得た。このとき、∠ABCの角度の最確値の標準偏差の値はア となる。
また、表3の測定値の最確値を∠ABCの角度とし、辺ABの辺長を3.0m、辺BCの辺長を8.0mとしたとき、辺CAの辺長は イ となる。
| 表3 |
|---|
| 測定値 |
| 59°59’57” |
| 60° 0′ 1” |
| 59°59’59” |
| 60° 0′ 5” |
| 59°59’58” |
| ア | イ | |
| 1 | 1.4″ | 7.0m |
| 2 | 1.4″ | 9.8m |
| 3 | 2.8″ | 5.6m |
| 4 | 2.8″ | 9.8m |
| 5 | 3.2″ | 7.0m |
解答
正解は5です。
| ア | イ | |
| 1 | 1.4″ | 7.0m |
| 2 | 1.4″ | 9.8m |
| 3 | 2.8″ | 5.6m |
| 4 | 2.8″ | 9.8m |
| 5 | 3.2″ | 7.0m |
解説
アの求め方
そもそも、最確値とは最も確からしいと考えられる値であり、一般的に最小二乗法で求めた値ですが、
今回の問題では同一条件での観測ですので、最小二乗法ではなく算術平均で十分です。
| 表3 |
|---|
| 測定値 |
| 59°59’57” |
| 60° 0′ 1” |
| 59°59’59” |
| 60° 0′ 5” |
| 59°59’58” |
(59°59’57”+60°00’01”+59°59’59”+60°00’05”+59°59’58”)÷5…
のように単純に計算しても構いませんが、秒にのみ着目することで簡単に導出できます。
しかしながら、煩雑な計算はミスを誘発しやすいので、簡単な式に置き換えることを推奨します。
各測定値の秒に着目し、すると
| 表3 |
|---|
| 測定値 |
| 59°59’57” |
| 60° 0′ 1” |
| 59°59’59” |
| 60° 0′ 5” |
| 59°59’58” |
→
| 秒” | |
| 60+ | -3 |
| 1 | |
| -1 | |
| 5 | |
| -2 |
上記秒の赤字7+11+9+15+8=50
測定値の回数は5回なので、50÷5=10
秒数50+10=60より、測定値平均(最確値)は60° 00′ 00″。
また、最確値がわかったのでそのまま2乗することで標準偏差のを求めることができます。
| 秒” | |
| 60+ | -3 |
| 1 | |
| -1 | |
| 5 | |
| -2 |
→
| 秒” | δ | δ2 |
| 60+ | -3 | 9 |
| 1 | 1 | |
| -1 | 1 | |
| 5 | 25 | |
| -2 | 4 |
最確値の計算についての解説はこちら
最後に標準偏差を求めます。
√(Σ δ2÷n(n-1))
=√(40÷5(5-1))
=√(40÷(5×4))
=√2
=1.4
よって、最確値の標準偏差は1.4”であることがわかりました。
イの求め方
イの求め方に入る前に注意するポイントが1つあります。
それは、アで求めた最確値の利用です。
他の試験等では答えを次の問題のヒントにすることはありますが、
測量士補の試験ではこの問のように計算過程の結果を利用することで導出できる答えが多いです。
よって、注意しながら問題を読み進める必要があるでしょう。
話がそれましたが、、、
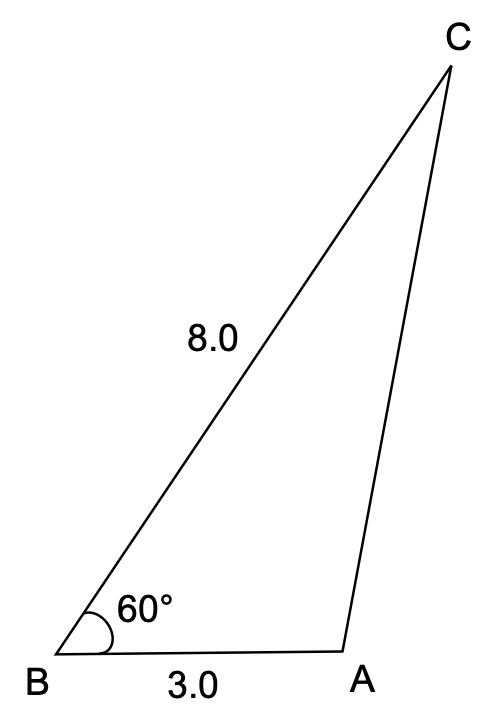
三角形ABCで∠ABCの角度を同じ条件で5回測定し、表3の結果を得た。このとき、∠ABCの角度の最確値の標準偏差の値はア となる。…∠ABC=60°
また、表3の測定値の最確値を∠ABCの角度とし、辺ABの辺長を3.0m、辺BCの辺長を8.0mとしたとき、辺CAの辺長は イ となる。
問題文の条件とアの導出より、図形を書いてみます。
そして、2辺とその間の1角がわかったので、余弦定理より
CA2 = 32 + 82 -2 × 3 × 8 × cos60°
= 9 +64 – (48 × 1/2 )
= 73 – 24
= 49
CA = 7 m
以上より、イの選択肢が7.0mであることがわかりました。

