測量士補試験 令和5年第7問

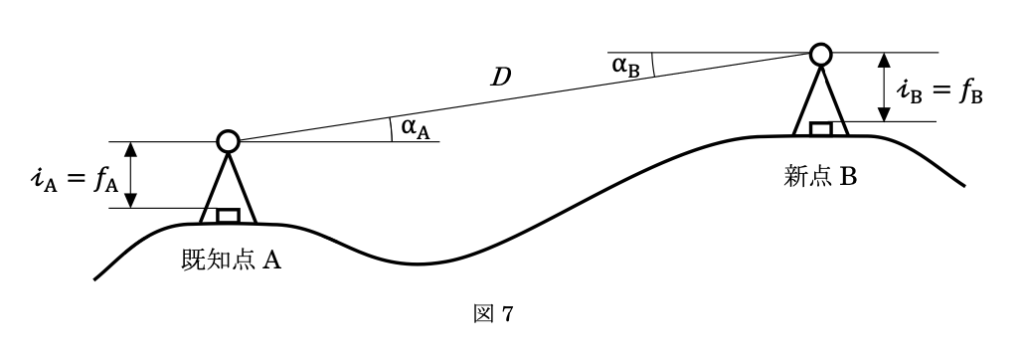
　公共測量におけるトータルステーションを用いた1級基準点測量において、図7に示すように、既知点Aと新点Bとの間の距離及び高低角の観測を行い、表7の観測結果を得た。Dを斜距離、α_Aを既知点Aから新点B方向の高低角、α_Bを新点Bから既知点A方向の高低角、i_A、f_Aを既知点Aの器械高及び目標高、iB、fBを新点Bの器械高及び目標高とするとき、新点Bの標高は幾らか。最も近いものを次の中から選べ。
　ただし、既知点Aの標高は10.00mとし、Dは気象補正等必要な補正が既に行われているものとする。
　なお、関数の値が必要な場合は、巻末の関数表を使用すること。

１．190.71 m
２．190.81 m
３．200.71 m
４．200.81 m
５．204.28 m

解答
解説

解答

正解は３です。

選択肢
１．190.71 m
２．190.81 m
３．200.71 m
４．200.81 m
５．204.28 m

解説

まず解説に入る前に、表の条件を図示して整理してみます。

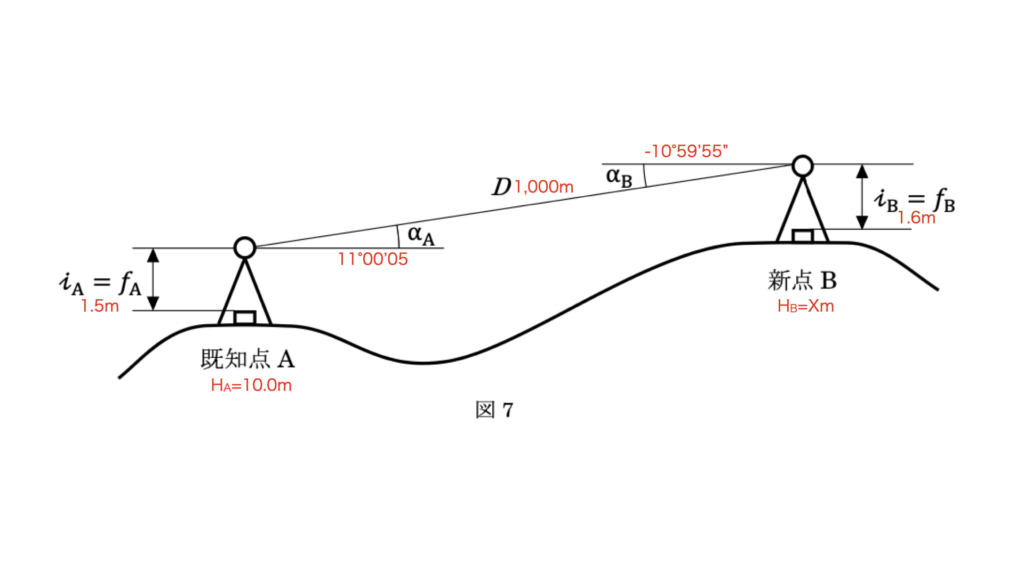
同様の問題において、両差が不明であることが本問題の鍵です。
したがって、2方向からの観測の両差を等しいものと仮定して、新点Bの標高を導いていきます。

両差をKとおく。

➀正方向観測（既知点A→新点B）
H_B = H_A + i_A + Dsinα_A – f_B + K

➁反方向観測（新点B→既知点A）
H_B = H_A + f_A – Dsinα_B – i_B – K

➀と➁の式を足すと
2H_B = 2H_A+ i_A+ f_A+ Dsinα_A– Dsinα_B– f_B– i_B
2H_B = 2H_A+( i_A+ f_A)+ D(sinα_A– sinα_B)–( f_B+ i_B)
2H_B = 2×10.0+(1.5+1.5)+1,000×2×0.19081–(1.6+1.6)
2H_B = 23+381.62-3.2
2H_B = 401.42
H_B = 200.71

本問は複雑で測量士補試験の中でも難しい問題だと思います。